Compressed air; theory and computations . (I) is completely satisfied—that is—given any two of x, y and z the third will be found on the lineCD laid over the two given. Note that the line AE is unnecessary—it being placed in thefigure for demonstration only. Note also that the line FG is notto appear on the chart and that the factor C effects only the widthof the chart and may be taken to suit convenience. Evidently this solution applies only to the special case whenn — m + r. It has the further objection that if the corre-sponding numerical values of x, y and z are very different thenthe leng
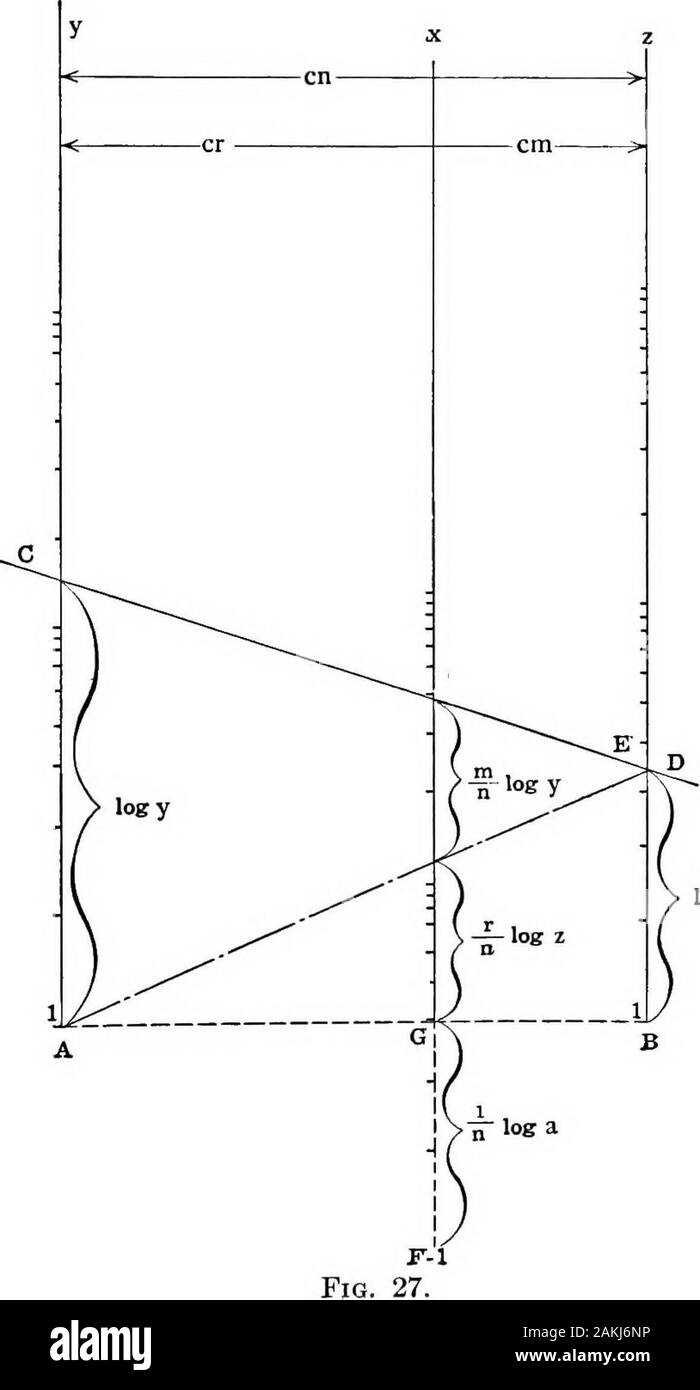
Image details
Contributor:
The Reading Room / Alamy Stock PhotoImage ID:
2AKJ6NPFile size:
7.1 MB (115 KB Compressed download)Releases:
Model - no | Property - noDo I need a release?Dimensions:
1160 x 2154 px | 19.6 x 36.5 cm | 7.7 x 14.4 inches | 150dpiMore information:
This image is a public domain image, which means either that copyright has expired in the image or the copyright holder has waived their copyright. Alamy charges you a fee for access to the high resolution copy of the image.
This image could have imperfections as it’s either historical or reportage.
Compressed air; theory and computations . (I) is completely satisfied—that is—given any two of x, y and z the third will be found on the lineCD laid over the two given. Note that the line AE is unnecessary—it being placed in thefigure for demonstration only. Note also that the line FG is notto appear on the chart and that the factor C effects only the widthof the chart and may be taken to suit convenience. Evidently this solution applies only to the special case whenn — m + r. It has the further objection that if the corre-sponding numerical values of x, y and z are very different thenthe lengths of the x, y and z lines will be different, though notin the same proprtion. The chart will have a better appearanceif the three lines are nearly equal. The general solution is as follows (See Fig. 28): 172 APPENDIX B Let I = desired length of chart in inches, k = desired width of chart in inches, %i = greatest value of x to appear on the chart, fx be the necessary multiplier for logs x, to give desired length to the x line. 173. log z Then fx (log Xi - - log a) = I. Whence fxLet 21 = be the value of z corresponding with xu CII) 174 COMPRESSED AIR Let /s be the nearest whole number to I (HI) logzi that being the most convenient multiplier forlogs of z to make the z line nearly equal to thex line. £ i z f y log y -ffyiosy ^ I k fz IOB z x f z log z 1(» f 1 r-i Fig. 28. Let fv be the necessary multipher of logs y. We have yet to find p, q and /„. Imposing the condition that Eq. (I) must be satisfied andremembering that all values of log x are to be multiplied by /».Then must APPENDIX B 175 |/*logz = T - fx log z. Whence p ?n = r-ffk (IV) also |/ylogy ^ — fx log y. Whence /„ n q (V) EvidentlyExampt q*=k-p (VI)!e.—Design a chart to solve the formula for friction in air^pipes, viz., . 0.1025 vH3 rd6-31 X 3, 600 in which / = loss of pressure in pounds per square inch, I — length of pipe in feet, v = cubic feet of free air per minute, r = ratio of compression = n