An elementary treatise on coordinate geometry of three dimensions . torsion. Again, tan 6 = , , = A, and therefore 0 is constant.0 1 -rip This problem was first investigated by Bertrand, and curves whichsatisfy the conditions are on that account called Bertrand curves. Ex. 10. A curve is projected on a plane the normal to which makes angles a. and j3 with the tangent and binomial. If p[ is the o 00s Ljradius of curvature of the projection, prove that p — . .. 298 COOKDINATE GEOMETEY fcH. XIV. Let P be a point of the curve and Q and R the points of the curve distant 8s from P. Then, if the area
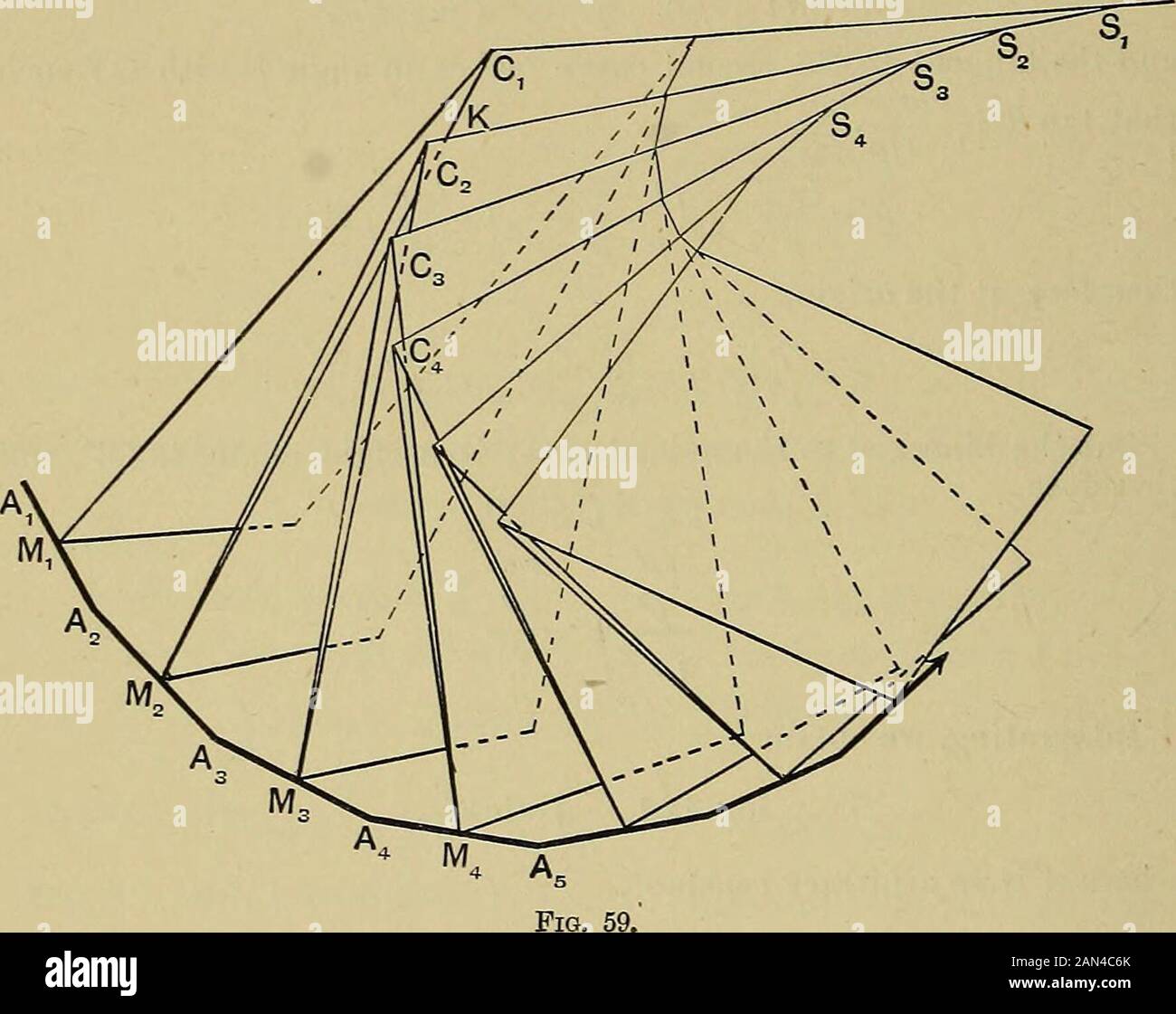
Image details
Contributor:
The Reading Room / Alamy Stock PhotoImage ID:
2AN4C6KFile size:
7.2 MB (229.9 KB Compressed download)Releases:
Model - no | Property - noDo I need a release?Dimensions:
1775 x 1408 px | 30.1 x 23.8 cm | 11.8 x 9.4 inches | 150dpiMore information:
This image is a public domain image, which means either that copyright has expired in the image or the copyright holder has waived their copyright. Alamy charges you a fee for access to the high resolution copy of the image.
This image could have imperfections as it’s either historical or reportage.
An elementary treatise on coordinate geometry of three dimensions . torsion. Again, tan 6 = , , = A, and therefore 0 is constant.0 1 -rip This problem was first investigated by Bertrand, and curves whichsatisfy the conditions are on that account called Bertrand curves. Ex. 10. A curve is projected on a plane the normal to which makes angles a. and j3 with the tangent and binomial. If p[ is the o 00s Ljradius of curvature of the projection, prove that p — . .. 298 COOKDINATE GEOMETEY fcH. XIV. Let P be a point of the curve and Q and R the points of the curve distant 8s from P. Then, if the area of the triangle PQR is denoted 1 2A 1 2A by A, -=Lt^. Similarly for the projection — = Lt ~-^-, where A, 6V are the projections of A and 8s. But A=Acos/3, and 8s = 8s sin a, whence the result. 205. Geometrical investigation of curvature and tor-sion. The following geometrical investigation of thecurvature and torsion of a curve is instructive. Let Ax, A2, A3, ... , (fig. 59), be consecutive vertices of anequilateral polygon inscribed in a given curve, and let. M1; M2, M3, ... be the mid-points of the sides. PlanesM-lC^, M2C2S2, ... are drawn through Mx, M2, ... normal tothe sides. M1C1, M^ are the lines of intersection of theplanes M1C1S1, M2C2S2 and the plane A^Agj similarly, M2C2and M3C2 lie in the plane A2A3A4, and so on. Then Cx is the centre of the circle through the pointsA1? A2, A3, and its limiting position when A2 and A3 tendto A2 is the centre of curvature at Ar Let p denote the §205] GEOMETRICAL [NVE8TIGATION 200 radius of the circle of curvature at a, . From the cyclicquadrilateral c^MjA^m., , *i*i =C A 2siu | M^jM, [ - But since the limiting positions of AjA., and a.a. aretangents, AXA2 _ ds_ 2 sin M^Mg ~~ dJ/Therefore, since the limiting value of CXK is p, dsp = d$ and the curvature=-—=-, where p is the radius of thecircle of curvature. Since the planes MjC^, MoCjSj are at right angles tothe plane A1A2A3, their line of intersection CjSj is normalto the pla